5/11/2009
Firma Electric Alchemy wykorzystała usługi chmury obliczeniowej Amazon EC2 i program Elcomsoft Distributed Password Recovery do łamania haseł w plikach PGP ZIP, formacie stosowanym przez komercyjną wersję pakietu PGP. Na zwykłym, stacjonarnym komputerze szacowany czas złamania hasła został określony na 2100 dni. W chmurze wartość ta zmalała do 122 dni.
Klaster do łamania haseł
Jedna maszyna uruchomiona na EC2 jest w stanie sprawdzać 500 tys. haseł na sekundę, a godzina jej pracy kosztuje jedyne 0,10 USD. Łatwo więc obliczyć, że jedna wirtualna maszyna łamie hasło w 3600 dni (a więc wypada słabiej od stacjonarnego komputera).

Po dodaniu kilku maszyn, z 3600 dni robi się 122
Jeśli jednak dodamy 10 kolejnych kopii wirtualnej maszyny o większej mocy obliczeniowej (koszt 0,30 USD za maszynę), uzyskamy zadowalający nas wynik przeszukania całej przestrzeni kluczy w 122 dni, za 3 USD za godzinę. Jak się okazuje, można sobie całkiem tanio zbudować superkomputer na miarę NSA ;-)
Koszt złamania hasła
Firma pokusiła się o przedstawienie kosztu pracy “chmurowego” łamacza haseł. Dane dla haseł składających się z małych liter od a do z prezentują się następująco:
- Złamanie 8 znakowego hasła – koszt 3 USD.
- Złamanie 9 znakowego hasła – koszt 87 USD.
- Złamanie 10 znakowego hasła – koszt 2300 USD.
- Złamanie 11 znakowego hasła – ~60 tys. USD
- Złamanie 12 znakowego hasła – koszt prawie 1,5 mln USD
Użycie cyfr w haśle podnosi oczywiście koszty łamania. W przypadku 9-cio znakowego hasła składającego się z małych liter (a-z) i cyfr, koszt łamania w chmurze wyniesie nie 87 USD a 1600 USD. Jakie hasło zatem warto wybrać, żeby jego złamanie było dla atakującego najdroższe? Oto odpowiedź:
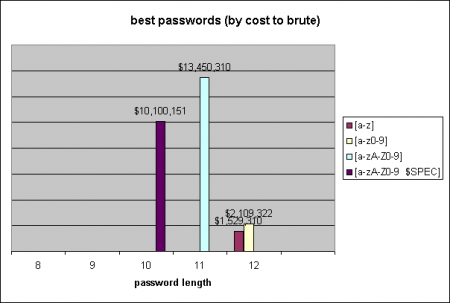
Wykres autorstwa firmy ElectricAlchemy
Pamiętajcie, że PGP ma całkiem mocne algorytmy szyfrowania. Ile czasu zajmie więc złamanie “domowych” szyfrów lub słabszych algorytmów stosowanych w innym oprogramowaniu? No właśnie…



 Weź udział z kolegami w jednym z naszych 8 cyberwykładów. Wiedzę podajemy z humorem i w przystępny dla każdego pracownika sposób. Zdalnie lub u Ciebie w firmie. Kliknij tu i zobacz opisy wykładów!
Weź udział z kolegami w jednym z naszych 8 cyberwykładów. Wiedzę podajemy z humorem i w przystępny dla każdego pracownika sposób. Zdalnie lub u Ciebie w firmie. Kliknij tu i zobacz opisy wykładów! Każdy powinien zobaczyć te krótkie szkolenia! Niektóre z nich są darmowe. Wszystkie to praktyczna wiedza i zrozumiały język. 6 topowych tematów — kliknij tutaj i zobacz szczegółowe opisy.
Każdy powinien zobaczyć te krótkie szkolenia! Niektóre z nich są darmowe. Wszystkie to praktyczna wiedza i zrozumiały język. 6 topowych tematów — kliknij tutaj i zobacz szczegółowe opisy.
W ostatnim akapicie jest chyba sugestia, że popularne rozwiązania przeznaczone do nieprofesjonalnych zastosowań są mniej bezpieczne – ale to nie do końca prawda. Wszystko zależy od stosowanych algorytmów. “Domowe” rozwiązania często stosują te same algorytmy – te uznane we współczesnej kryptografii za bezpieczne: do szyfrowania symetrycznego RSA albo ElGamal a do asymetrycznego prawie wszędzie obecnie AES (Rijndael). To, że “poważne” PGP używa takich algorytmów wcale nie świadczy o tym, że jest jakoś wyjątkowo “mocne”. Domowe, darmowe rozwiązania też ich używają jak np. TrueCrypt, Openssl, GnuPG.
Przemysław: W żadnym wypadku nie zamierzałem sugerować, że TrueCrypt, OpenSSL, czy GnuPG (z wszystkich trzech korzystam na co dzień) są “gorsze” od PGP. Na myśli miałem raczej oprogramowanie z tzw. “domową” kryptografią, czyli coś z gatunku “Jan wpada na pomysł wymyślenia szyfru, który będzie najlepszy”!
Pisząc “słabsze” miałem chociażby na myśli bazy haseł programów takich jak WinFTP czy TotalCommander (AFAIR oparte o jakieś przestarzałe szyfry z króciutkimi kluczami). Niestety, jak wiadomo, to właśnie z takich programów użytkownicy korzystają częściej niż z PGP czy TrueCrypta…
Ja niby inżynier jestem ale nie rozumiem ostatniego wykresu :(
Czy mam go rozumieć tak, że najtrudniejsze do złamania hasło jedenasto-znakowe to takie składające się z [a-zA-Z0-9] (czyli bez znaków specjalnych)? Dlaczego to ze znakami specjalnymi będzie łatwiej złamać?
A może chodzi o to, że generalni najtrudniejsze do złamania hasło to [a-zA-Z0-9]{11} ? Wtedy raz – jak wyżej, dwa – dlaczego nie dłuższe?
Jeżeli po prostu mam takie braki z podstaw kryptografii, że niczego nie rozumiem, to powiedzcie – pójdę płakać w kąciku :)
@Damian:
To panie inżynierze, pan popatrzy na kolorki, bo moim zdaniem pomyliłeś słupki ;-)
Anyway ten wykres wygląda trochę kiepskawo. Jakby ktoś excela nie umiał używać i na dodatek pisał ten artykuł “na chybcika” żeby go przypadkiem ktoś nie uprzedził :P
@Radek: raczej nie rysowali tego na szybcika, bo to ich autorska praca ;-)
@Radek
Nie no jak to… Najwyższy pasek to [a-zA-Z0-9]{11}. Drugi w kolejności to [a-zA-Z0-9 $SPEC$]{10}, następny [a-z0-9]{12} i najniższy [a-z]{12}.
Proszę Was, bądźcie chmurą, która wesprze mój brak kapowania :)
Muszę zgodzić się z Panem inżynierem. Z tego wykresu nie da się zbyt wiele odczytać :). Takie opracowanie wyników pomiarów nie przeszłoby nawet w podrzędnym technikum :). Nie można na nim zaobserwować chociażby charakteru zmian wartości funkcji kosztu w zależności od danego jednego parametru bo każdy, z (aż) czterech słupków, obrazuje wynik pomiaru przy zmienionych wszystkich dwóch parametrach (ilośc znaków, długość hasła).
Badania mimo wszystko interesujące.
Panowie, w żaden sposób nie chce usprawiedliwiać autorów raportu, ale ten wykres służy do zobrazowania czy lepsze jest krótkie skomplikowane hasło, czy może dłuższe łatwiejsze do zapamiętania (bez znaków specjalnych).
Wniosek nasuwa się sam: masz dziesięcioznakowe hasło “losowe”, trudne, ze znakami specjalnymi (a więc na pewno masz problem, żeby je zapamiętać). Pozbaw je znaków specjalnych i wydłuż o jeden znak — dzięki temu zwiększysz swoje bezpieczeństwo (w rozumieniu kosztu łamania twojego hasła w chmurze), a przy okazji hasło będzie łatwiejsze do zapamiętania.
Ok ja już rozumiem :) Zmylił mnie tytuł “best passwords” – to po prostu porównanie kilku przykładów. Dzięki Piotr za wyjaśnienie!
Ja tam jakoś nie mam problemów z zapamiętaniem hasła… Teraz pozostaje kwestia tego ile jest znaków a-z, ile jest znaków A-Z i ile jest znaków specjalnych. Jeżeli znaków specjalnych jest więcej niż znaków A-Z * a-z to hasło byłoby trudniejsze do złamania. W przeciwnym wypadku hasło jest łatwiejsze. Tu należałoby podejść z zasadą mnożenia z kombinatoryki. Przyjmijmy że ilość znaków (A-Z) * (a-z) jest większa niż ilość znaków specjalnych. Mamy wtedy dla 4 znakowego hasła ze znakami specjalnymi 4*[(A-Z)*(a-z)*(0-9)*spec]=4*[(A-Z)*(a-z)*(0-9)]+4*spec; Dla 5 znaków bez znaków specjalnych mamy 5*[(A-Z)*(a-z)*(0-9)]=[(A-Z)*(a-z)*(0-9)]+4[(A-Z)*(a-z)*(0-9)]; Trzeba teraz zauważyć że żeby to działało to [(A-Z)*(a-z)*(0-9)] musi być większe niż 4*spec; Przy czym jest większe ponieważ ilość znaków (0-9) to 10 czyli 10*(A-Z)*(a-z), a z założenia mamy że (A-Z)*(a-z) > spec; Przy czym (A-Z) to ilość znaków od A-Z, (a-z) to ilość znaków od a-z i (0-9) to ilość znaków 0-9.
@Dariusz
Btw. Liter jest 27… zatem kombinacji wielkich i małych liter dla jednego znaku w haśle to 729. A 729 to więcej kombinacji niż kombinacji dla jednego znaku ze znaków ascii, których jest 256.
[…] Łamanie haseł w chmurze […]
[…] PGP ;-) A jeśli kogoś nie stać na 2500 konsol PS3, zawsze może wybrać niskobudżetową wersję łamania haseł w Chmurze Amazonu, o której pisaliśmy parę tygodni temu. jeden z prywatnych klastrów […]
[…] (Jest też wersja tańsza, 40 min. za 17 dolarów). Całkiem niedawno pisaliśmy o niskich kosztach łamania haseł w chmurze — sprawdź ile kosztuje (i jak długo trwa) łamanie innych […]
Chwila,moment – Dariusz!
Podstawy kombinatoryki nie zmieniły się od 70-tych lat ubiegłego wieku ,gdy to przerabiałem.
Spróbuję “łopatologicznie”:
zbiór elementów (znaków mogących uczestniczyć w tworzeniu hasła) – 27(alfabet liter małych)+27(alfabet liter dużych)+10(cyfry)+36(wziąłem na chybił trafił- to nie jest takie ważne) = 100 (zaokrągliłem).
Przy 100 elementach i (powiedzmy) haśle 10 elementowym (z powtórzeniami) otrzymujemy bazę haseł do odgadnięcia … kalkulator mi padł to podam ostateczne wyliczenie : (100*101*102*104*104*105*106*107*108*109)/10!(silnia).
Teraz podzielcie tą liczbę przez 500 tys. haseł na sekundę i otrzymamy czas “skanowania” całej bazy haseł w poszukiwaniu … straconego czasu! Powodzenia! Jak by ktoś wątpił w sens moich wyliczeń – niech napisze e-maila – odpuscsobie@mnietyz.pl.
Ale czad (tzn. chmura).
Podstawy kombinatoryki się nie zmieniły, zmienił się tylko ich obraz w Twojej pamięci, ale wujek Google by Ci go przypomniał, gdybyś tylko go o to poprosił… ;]
http://pl.wikipedia.org/wiki/Kombinacja_z_powtórzeniami
http://pl.wikipedia.org/wiki/Wariacja_z_powtórzeniami
podsumowując, poprawny wynik to: 100 do potęgi 10-tej, czyli ok. 6341958 lat.
W Polsce też mamy podobne serwisy hashbreaker.pl można łamać hashe haseł za poomocą RT, można płacić SMSem, a średni czas oczekiwania na hasło to 120 minut…
Nie wiem czy takie koszty są faktyczne, bo jeśli hasło na przykład może być wpisywane ciągle to trwać może chwilę jego odgadnięcie. Jeśli po złej próbie jest blokada wpisania hasła to już pojawia się pewien problem lub spowolnienie, następnie odcinanie adresu na x czasu z błędnym hasłem. To wydaje się stałą walką, między łamaniem zabezpieczeń i powstawaniem dodatkowej trudności do ich złamania. Z czasem lub być może nawet już, sama hasła do banku nie wystarczą tylko trzeba będzie robić 3 warstwowe przejścia jak hasło + wybrany element z puli graficzny + hasło elektroniczne lub coś takiego typu.